UniV3 LP: Calculating Price Range

How to choose a ±% range when LPing on Uniswap

How do you LP on UniV3 with a ±% range? E.g. if you wanted ±30% should you do:

1. \(Lower: P \times 70\text{%}\)
   \(Upper: P \times 130\text{%}\)

   or

2. \(Lower: \frac{P}{1.3}\)
   \(Upper: P \times 1.3\)

Let's find out!👇

The upper price is the same since P * 130% = P * 1.3

But what about the lower price? Should it be 70% or 76.9%? (76.9% = 1/1.3)

It turns out that only one of these is correct! Let's analyze.

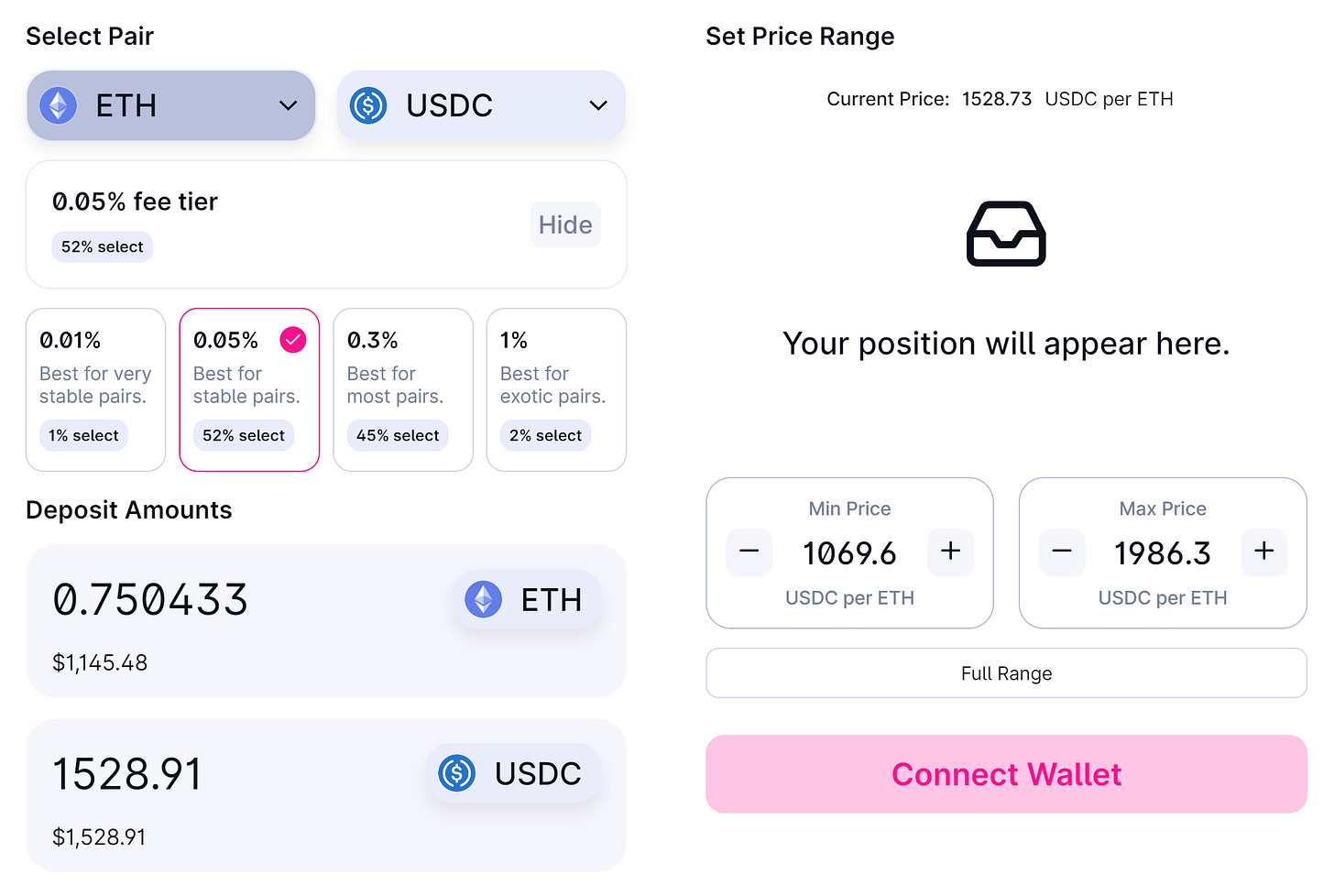
• Pool: ETH-USDC

• Price: $1,528

• Our capital: split evenly (1 ETH and 1,528 USDC)

Let's try method 1 for a ±30% range: LP between 70% ($1,069) and 130% ($1,986).

*Spoiler alert: we can’t!* When we go to Uniswap it won’t let us LP all our capital. In fact, it will only let us deposit 0.75 ETH. That's 1/4 of our ETH not earning any yield!

Now let's try method 2.

Since 1/1.3 = 76.9% and 1.3 = 130%, we LP between 76.9% (~$1,176) and 130% ($1,986).

Uniswap lets us deposit all our capital. Success!

So why is the lower range P / 1.3 rather than P * 70%?

It turns out that we have to follow the equation:

\(\frac{lower}{P} = \frac{P}{upper}\)

E.g. if the lower range is 2/3 of P, then P must be 2/3 of the upper range.

See @atiselsts paper (3.2.2) for more here.

This seems unintuitive 🤔 Why can’t we simply do ±30% of P?

The answer is that we are working with tick math, which involves exponents. So LP ranges are linear in “tick space”, but non-linear in “price space”. There is a direct mapping between ticks and prices in UniV3:

\(Price = 1.0001 ^ {Tick}\)

A price of $1,528 corresponds to tick 73,325 (since 1.0001 ^ 73,325 ≈ $1,528).

If we LP on tick 73,325 with ±2,620 ticks, we get:

\(Lower: 1.0001 ^ {73,325 - 2,620} ≈ $1,176\)

\(Upper: 1.0001 ^ {73,325 + 2,620} ≈ $1,986\)

Key Insights:

1. The math is ±ticks, not ±%. This generalizes to any LP range.

2. For any LP Strategy of width ±X% (we used X = 30%), the proper price range to fully utilize capital is:

   \(Lower: \frac{P}{\frac{X}{100} + 1}\)
   \(Upper: P \times (\frac{X}{100} + 1)\)

Caveats/Questions:

• Don’t forget to leave some tokens to pay for gas (e.g. ETH on Ethereum, MATIC on Polygon).

• How well do ±X% LP strategies perform?

• What is a good X to pick?­

---

Disclaimer: This content is for educational purposes only and should not be relied upon as financial advice.