How to hedge ANYTHING (including UniV3 LP positions) with options

A tutorial on hedging payoffs using options

Brandon

Mar 20, 2023

View on Twitter

How to hedge ANYTHING (including UniV3 LP positions) with options 👇

Why options?

Flexibility: Construct any payoff curve
Greater protection: hedge against price going up AND down
Capital efficiency: Low upfront cost for OTM puts/calls

Let's construct a hedge!

First, identify your strategy's position.

Assume initial ETH price is $1,000. Let's start with 1,000 USDC.

We sell 50% of that for ETH:

x0 = 0.5 ETH
y0 = 500 USDC

We LP 0.5 ETH & 500 USDC in the ETH-USDC pool.

Second, calculate the payoff curve for your strategy's position.

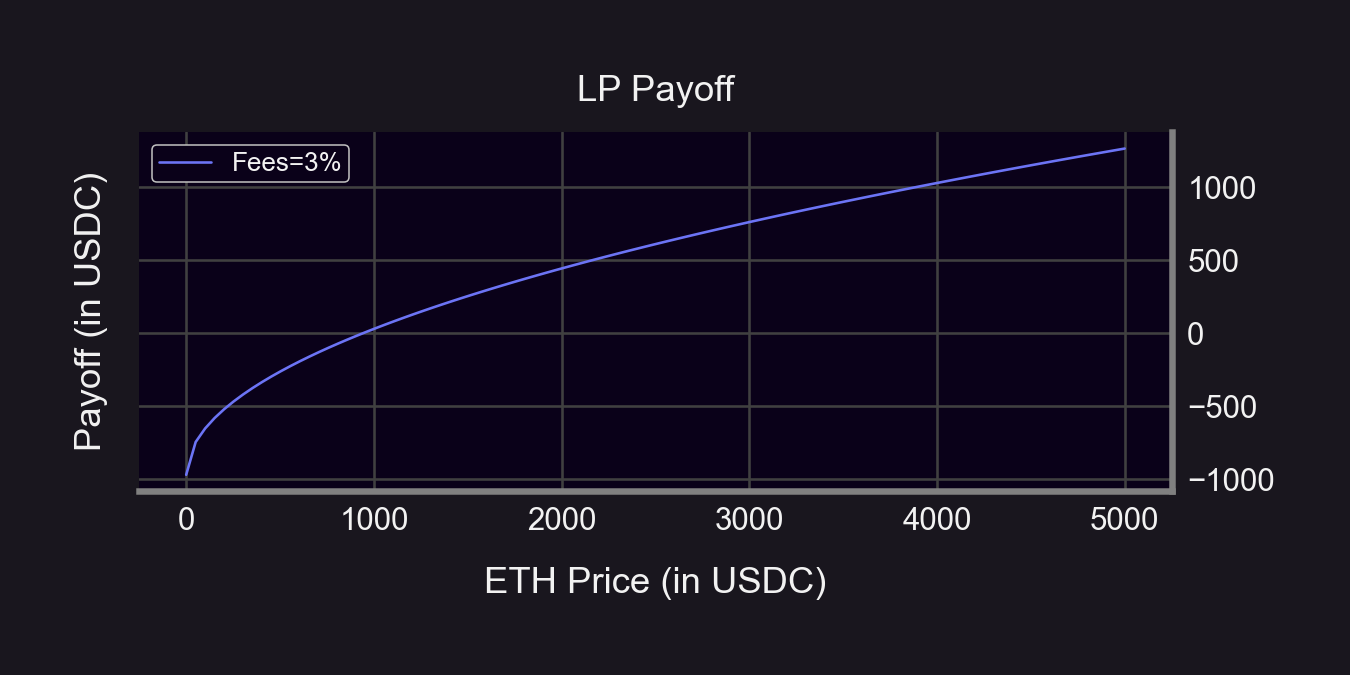
UniV2 LP value: V = 2L√S + fees
S = (Spot) price of ETH
L = √(x0 * y0)

Subtract our initial capital:

Payoff = 2L√S + fees - $1,000
Derivation by @p_e here

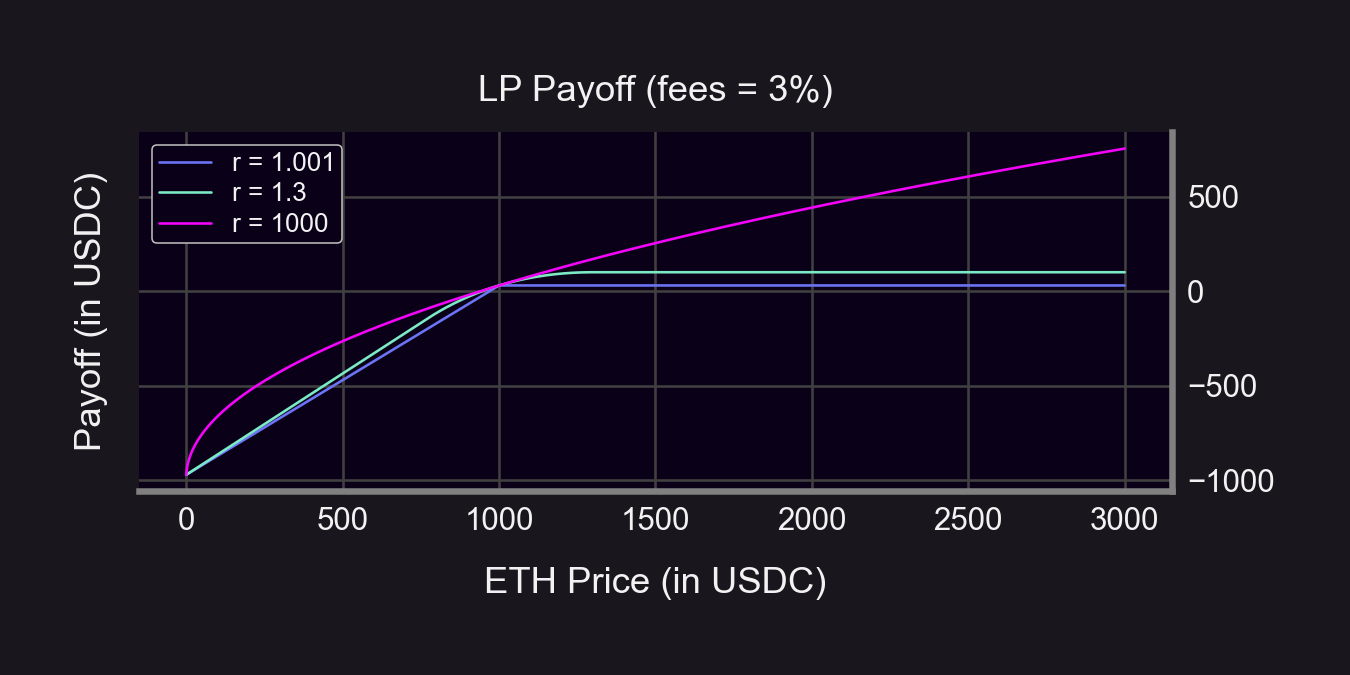
And for UniV3...

A *bit* more complicated than UniV2
Formula (while in range) by @guil_lambert here
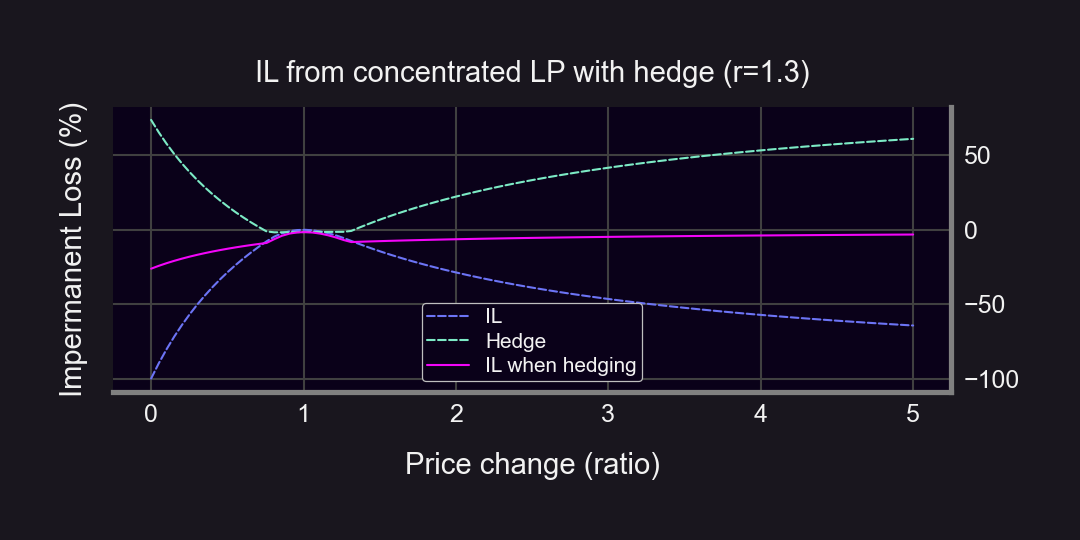
Example: r = 1.3 → ±30% LP range (see 🧵 for why)

Panoptic @Panoptic_xyz

1/13 Read our latest #ResearchBites from @brandonly1000 of the @Panoptic_xyz research team! ===== How do you LP on UniV3 with a ±% range? E.g. if you wanted ±30% should you do: 1) Lower: P * 70% Upper: P * 130% or 2) Lower: P / 1.3 Upper: P * 1.3 Let's find out!👇

$\begin{align} V(S)&=\frac{2\sqrt{K}r\left(\sqrt{S}-\sqrt{S_0}\right)-\left(S-S_0\right)}{r-1}+F,\\ \text{}\\ \text{where}&\\ \text{}\\ F&\text{= Accumulated fees},\\ K&=\sqrt{\text{PriceUpper}\cdot\text{PriceLower}},\\ S_0&=\text{Starting price},\\ r&=\sqrt{\frac{\text{PriceUpper}}{\text{PriceLower}}} \end{align}$

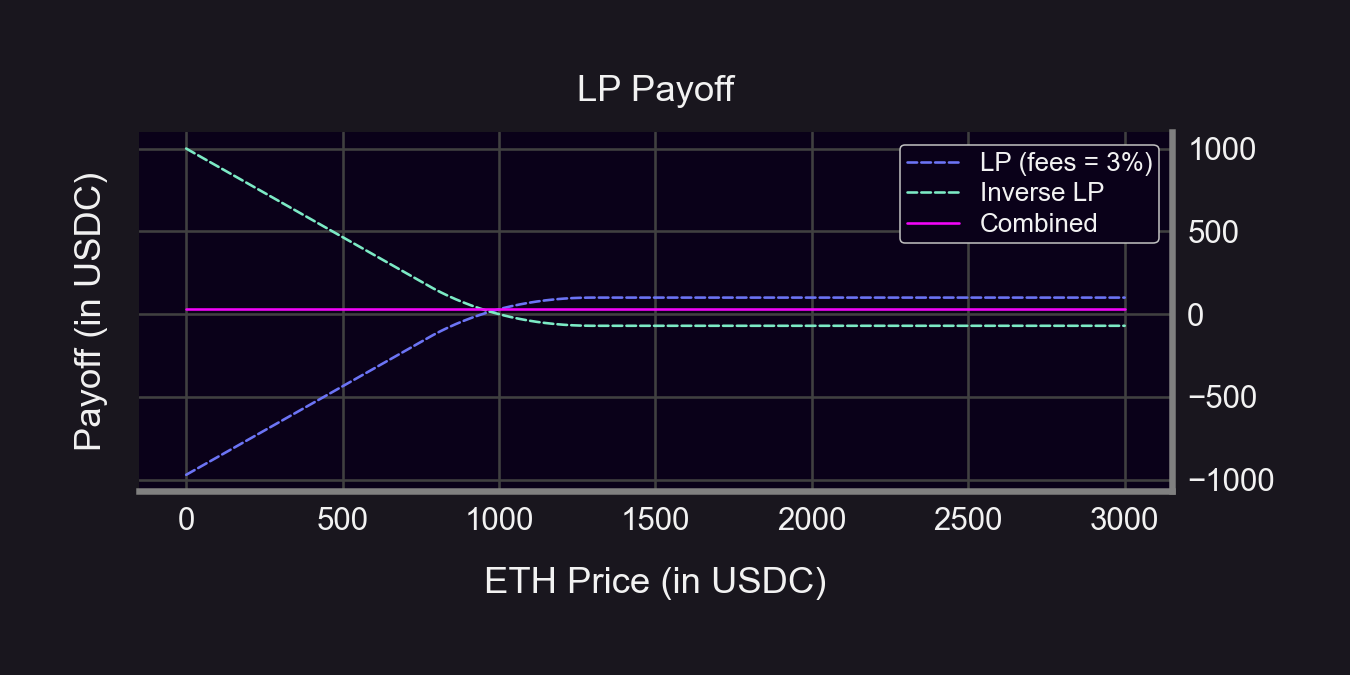
Third, find an "inverted" payoff curve.

You want to hold a portfolio that pays the opposite. So just flip the payoff curve on its head.

The goal is to #FlattenTheCurve into the pinkish line.

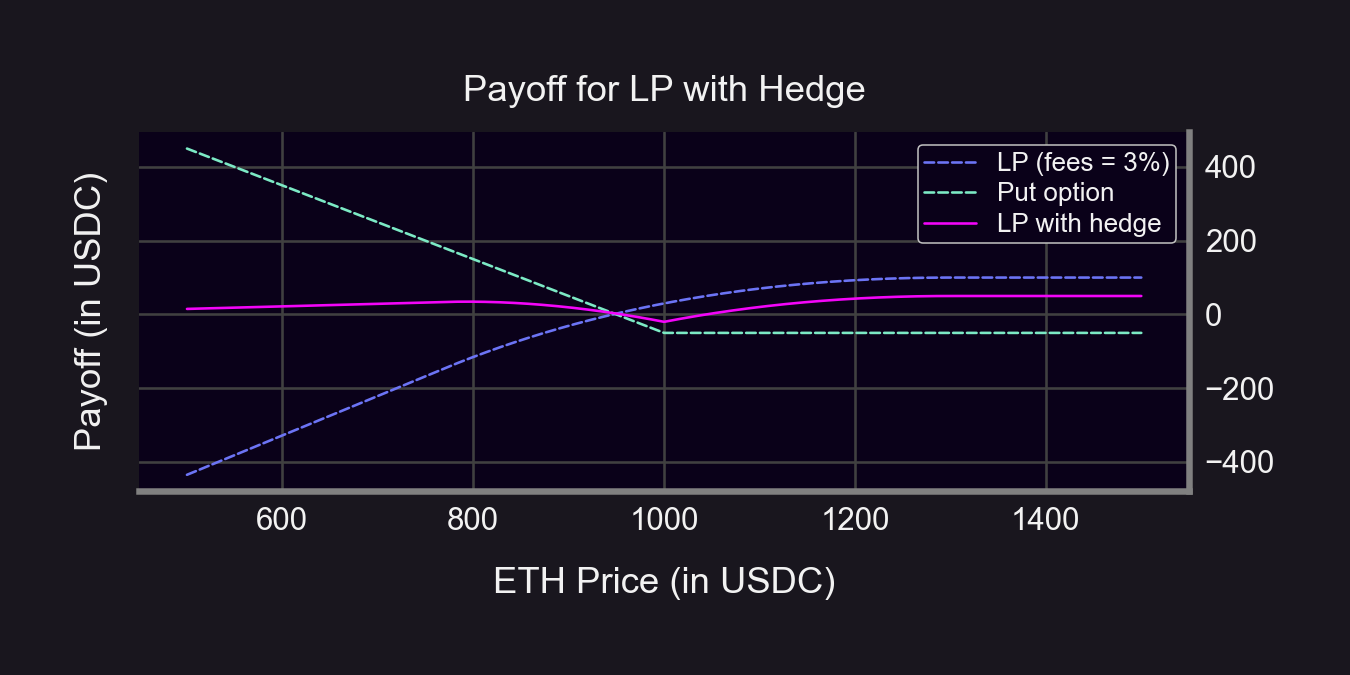
Example when r = 1.3 👇

Fourth, construct a portfolio replicating the inverse curve as closely as possible.

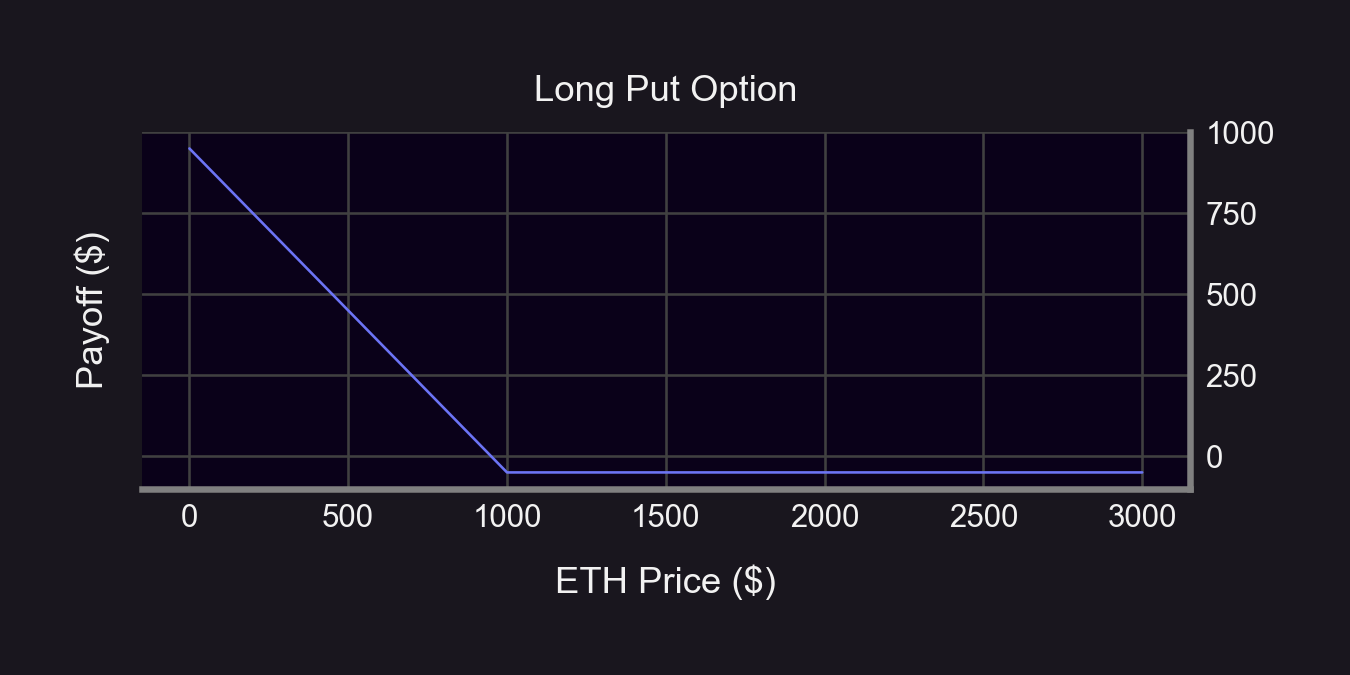
A long put option is a natural choice here since it benefits from $ movements down.

Finally, let's put them together. Buy the hedge portfolio and hold it with your original position!

Assumptions:

Initial ETH price = $1,000
Long 1 ATM Put (strike = $1,000, DTE = 10)
Put premium = $50
LP fees = 3% (r = 1.3 ⇔ DTE ≈ 10)

How'd we do?

S < $1,000: hedged payoff is flatter (and positive at times!)
S >= $1,000: hedged payoff is lower (due to premium)

Hedging always costs $. We need to earn enough fees to cover the hedge price.

To summarize:

Understand how your position reacts to price changes
Find an opposite reaction
Figure out what assets you can hold to mimic the opposite reaction (this is your hedge!)
Buy the hedge (with Panoptic😉)!
Take comfort knowing you're protected🛡️

What about impermanent loss (IL)?

Notice we started with 100% of our capital in USDC.
HODL portfolio of 100% USDC doesn't fluctuate
→ We already accounted for IL against a 100% USDC portfolio

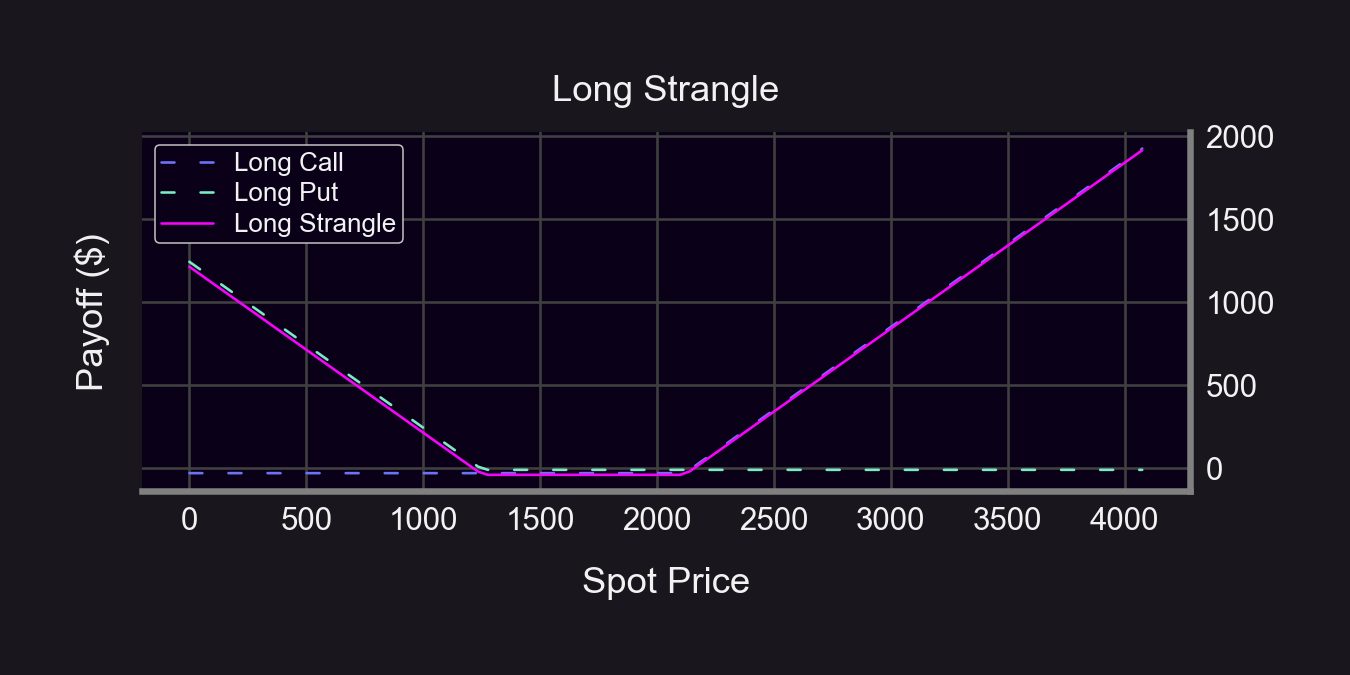
But if we define IL against a 50/50 ETH-USDC HODL, we can hedge with a strangle: