Composability, Perpetuity, and Oracle-Freeness in Panoptic

How Panoptic lets you trade multi-legged options without expiry and oracles

Every day we get closer to launch! 🤩

However, we heard some of you might have some Q's regarding Panoptions:

• How are they priced?

• Are they any different from Vanilla European Options?

• Why can't we just use Black-Scholes (BSM)?

Read our #ResearchBites to find out!

---

OK, first things first: Panoptic is a composable, perpetual ⌛️, oracle-free 🔮, instant-settlement options trading protocol📈 built on top of Uni V3. We're doing for decentralized options what x · y = k automated market makers did for spot trading 🎯🔥

To do this, we make use of the observation that LPing in Uni V3 (i.e. LPing ranged positions) has a very similar payoff curve as selling covered calls. Buying/selling options is intimately related to adding/removing liquidity

👆 We mentioned that Panoptic is:

• Composable

• Perpetual ⌛️

• Oracle-free 🔮

These 3 characteristics make Panoptic different from other protocols! Let's describe them briefly 👇

By "composable" we mean that users can create multi-legged options positions on a single mint! This allows for a wide variety of strategies that can be adjusted to each user's needs. Wanna know more about multi-legged positions? We got you *covered* 😉

Panoptic @Panoptic_xyz

1/25 DeFi Options Trading Is Powerful! There can be unlimited upside…😈 But also unlimited downside 😣 Every trader should know how to create these 18 options strategies in @Panoptic_xyz for any crypto asset, any strike, any size: ❤️ & rt 👇

Perpetual options have no expiration date & can be exercised at any time. This makes them more flexible than vanilla options. However, they can't be priced using Black-Scholes...but their pricing is based on a model that *does not require an oracle*

Why did we choose to not rely on a price oracle 🔮?

Cons of oracles:

• Need to provide reliable data 100% of the time

• Are complex to integrate on chain

• Can be expensive to maintain

👆 Difficult in DeFi! So how do we calculate the price without oracles? 🤔

Panoptic uses an oracle-free concept called streaming premium 🤓

• No upfront payment

• Instead, buyers pay a small fee at every block to keep their position open, whenever it is near-the-money

• This per-block fee is computed from every change in price of the asset 👇

Intuitively,

• If price changes a lot, volatility + fees are big

• If it doesn't change much, volatility + fees are small

Mathematically, the total premium corresponds to integrating theta (θ) of the option over time (with θ the rate of change of the option premium, P, with respect to time), se formula below.

\(\begin{align} \text{Premium } P&=\int_{\mathcal{S}(t)}\theta(S_t,K,\sigma )\mathrm{d} t\\ \theta(S_t,t)&=\frac{\partial V(S_t,t)}{\partial t}=\frac{S_t\sigma}{\sqrt{8\pi t}}\exp\left(-\frac{\left[\ln\left\{\frac{S_t}{K}\right\}+\frac{\sigma^2t}{2}\right]^2}{2\sigma^2t} \right)\\ &\text{here, $\sigma^2\in\mathbb{R}_{>0}$ is the volatility and $S_t$ is the asset price} \end{align} \)

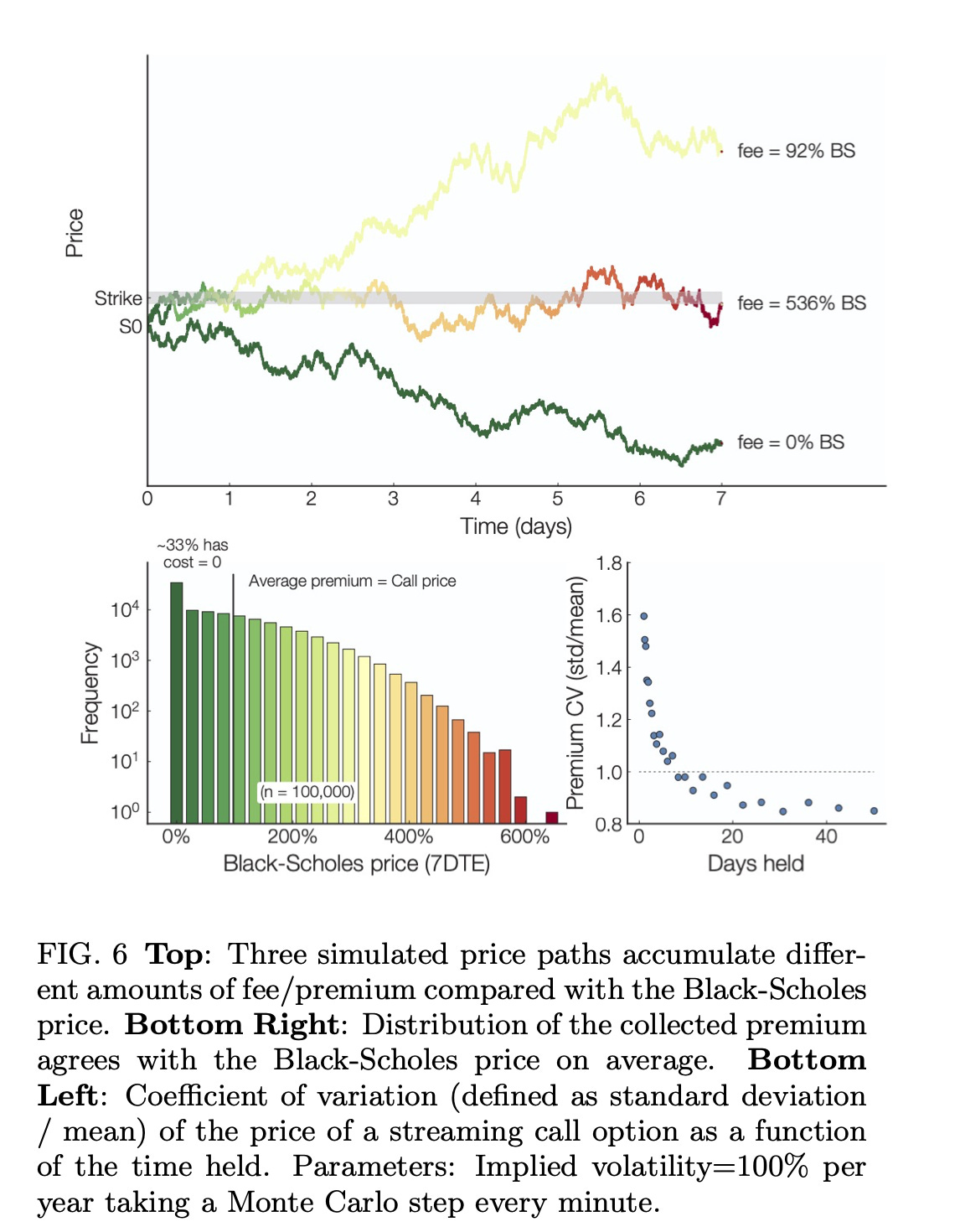
This corresponds to options that continuously expire at small time intervals (∆t). Does Panoptic integrate θ on-chain? No! 🙅‍♂️ In practice, this premia corresponds to the LP fees in the Uni V3 pool! Does this converge to BSM? Yes! 🤯 We can verify this w/ Monte Carlo 👇

Ok, so how do we implement this on chain? Using Uni V3-like structure!

• We keep track of fees + liquidity associated to each pos.

• As price moves, fees accumulate

• A buyer that opens at t1 & closes at t2 pays fees prop. to UniV3 fees (+ spread) between t1 & t2

  Indeed, UniV3 collects fees as

• \(\mathsf{totalFees}=\mathsf{fg_upper-fg_lower-fg_insideLast \cdot liquidity }\)

  where fgupper and fglower are the feegrouwthOutside0x128 of the upper and lower ticks in UniV3, and fginsdelast=feeGrowthInsde0lastX128, and liquidity is the liquidity owned by the protocol. In this setting, the option buyer would pay a premium as shown below to the seller:

  \(\mathsf{premium}=\frac{\mathsf{totalFees\cdot positionSize}}{\mathsf{liquidity}}\)

Detailed #ResesearchBites on the implementation soon 😉

---

😮‍💨 We tried hiding a lot of the "mathier" details, but we hope that wasn't too much to digest! If it was, or if you want to learn more about Panoptic, you can read our white paper here.